Bažant's Fraudulent theory exposed! The mathematics he used to explain the Twin Towers Collapse is WRONG!

: AE911Truth Staff; April 4, 2024

Author's note:

What follows is the first draft of a paper that has startling implications for the ongoing controversy about what really destroyed the Twin Towers on September 11, 2001.

While we wanted to share our preliminary findings with our supporters, we are still refining our calculations and will later be releasing a revised version of the paper, possibly with some changes in our mathematical analysis, though these changes will have no impact on the paper's ultimate conclusion.

Given the gravity of the World Trade Center issue and the revelations we've uncovered, we must proceed with the utmost diligence regarding our findings, as they will have serious ramifications on the future of the World Trade Center debate.

As soon as the final version of our paper is ready, we will publish it here on our site.

Thank you,

Roland Angle, P.E.

Chairman

Architects & Engineers for 9/11 Truth

Errors Revealed in Bažant's Calculations Further Bury the Official Story as ASCE and NIST Continue to Stonewall Calls for a New WTC Investigation

Just two days after the tragedy of September 11, 2001, engineering Professor, Zdeněk P. Bažant of Northwestern University submitted a paper to the ASCE's Journal of Engineering Mechanics attempting to explain why, following the airplane impacts, the Twin Towers collapsed.

His theory was later adopted by the National Institute of Standards and Technology (NIST) and incorporated into their final report on the destruction of the Twin Towers.

While Bažant's analysis has been criticized and challenged by AE911Truth and other researchers over the years for ignoring certain fundamental laws of physics, a new problem with his analysis has been discovered — the mathematical equation that Bažant devised to justify his theory contained glaring errors and inaccurate assumptions.

In other words, it's wrong.

The discovery was made by AE911Truth Chairman, Roland Angle, working with mechanical engineer Tony Szamboti. The two have written a paper outlining their findings. (See below)

On March 4, 2024, Angle and Szamboti submitted their paper via email to Professor Bažant, offering him the chance to respond by April 1 before the results of their findings were made public.

Despite having the opportunity to defend his calculations, as yet, Bažant has remained silent.

The discovery of these errors in Bažant's mathematical equation blasts yet another gaping hole in his contribution to the official story of the Twin Towers' destruction on September 11th, and further destroys the foundation on which NIST's faulty progressive collapse explanation was built.

We urge our supporters to share the following paper with others, particularly engineers, to impress upon them that the NIST reports were highly unscientific and merely papered over the easily observable evidence that explosives caused the Twin Towers' destruction. Knowledge about a crime is useless unless it's shared.

We ask that you help us by spreading this information far and wide!

(Link to PDF of the Paper).

PROFESSOR BAŽANT’S INCORRECT CONCEPT OF THE DESTRUCTION OF THE WTC TWIN TOWERS ON 9/11 AND ERRORS IN HIS MATHEMATICAL ANALYSIS INVALIDATE HIS THEORY AND THE NIST REPORT

By Roland Angle, Professional Civil Engineer

& Tony Szamboti, Professional Mechanical Engineer

March 4, 2024

On September 13, 2001, only two days after the attacks on September 11, 2001, Professor Zdenek Bažant of Northwestern University submitted a paper to the American Society of Civil Engineers (ASCE) publication JOURNAL OF ENGINEERING MECHANICS (JEM). His paper was titled Why did the World Trade Center Collapse? – Simple Analysis and was co-authored with one of his graduate students, Yong Zhou. This technical paper put forward a theory, which came to be known as the Crush Down Crush Up (CDCU) theory, that attempted to explain the mechanics of how the Twin Towers at the World Trade Center were destroyed on 9/11. The JEM published his paper in January 2002 after some additions were made. Since then, the CDCU theory has been adopted by the National Institute of Standards and Technology (NIST) as the official U.S. government explanation for the complete collapse of the Twin Towers.

This was the first of five papers¹ that Bažant and various co-authors produced between 2001 and 2022 to describe and defend his theory, and, as such, is the foundation that establishes the NIST narrative of the event and provides a mathematical analysis that attempts to provide proof of its validity.

An examination of Bažant’s first paper shows that the CDCU theory is not valid and the mathematical analysis Bažant presented as proof is flawed.

A close look at Why did the World Trade Center Collapse? – Simple Analysis

The official government report on the destruction of the towers, published in 2005 by NIST, only gave a hypothetical explanation for the initiation of the failures of the Twin Towers. The NIST Report did not describe the mechanics of the collapse and specifically endorsed Bažant’s theory to explain how the 110 story towers experienced complete collapse.²

According to NIST, the destruction of the Twin Towers can be explained as follows, and Bažant’s contribution will be noted:

The planes crashed into the towers severing some of the steel columns and damaging others in the zone of the aircraft impacts.
The debris from the planes tore the fireproofing off some of the steel floor trusses in the impact zones.
Fires caused by the explosion of the jet fuel erupted in the impact zones.
The floor trusses were weakened by the fires and sagged, pulling in the perimeter columns.

[At this point, the remainder of the NIST theory is provided by Bažant’s CDCU theory]

After burning for the next hour or so, the heat from the fires weakened the structure and the weight of the building above the fire and impact damaged zone overcame the ability of the damaged zone to bear the weight of the upper part of the building. The upper part of the building then fell down through the damaged zone and collided with the lower part of the building.
The force of the collision was sufficient to overcome the ability of the columns in the lower part of the building to withstand the impact.
The impact caused the lower part of the building to give way.
The destruction of the building continued all the way from the impact zone to the ground, driven by the falling weight of the upper part of the building, the mass of the damaged zone and the accumulating mass of the destroyed lower part of the building.
When the upper part of the building hit the debris below it on the ground, it was also destroyed.

Professor Bažant derived a number of mathematical equations in an attempt to prove his theory. This is a standard method in the engineering profession for asserting that a theory is valid, and consists of starting with known and accepted mathematical concepts and manipulating them, using logic, to arrive at mathematical statements that confirm the theory’s assertions.

Bažant began by describing his concept of the failure mechanism of the buildings. He started with what is known about the behavior of steel columns under vertical load: First, an elastic stage occurs wherein the columns bear the load but can recover to their original configuration; second, if the elastic reaction of the columns is overcome by the load, a plastic axial strain stage occurs in which the columns give way to a permanent deformation; and third, if the load is great enough to overcome the ultimate carrying capacity of the columns, a bending and buckling phase then occurs in which the columns fail and form plastic hinges as they are crushed by the load.

The first section of Bažant’s analysis examined the initial elastic response of the columns in the lower part of the building to the impact of the falling upper part of the building.

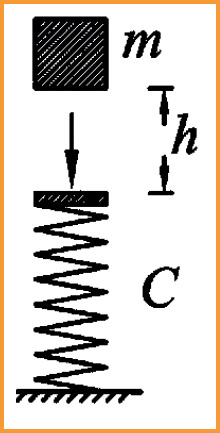
For this all-important analysis, Bažant produced an equation, identified as Equation (1), which he claimed could be used to prove that the buildings would not survive the elastic impact of the descent of the upper part of the building onto the lower part of the building. He identified the following entities that he claimed were necessary and essential elements of the elastic impact process:

The stiffness of the lower part of the building, represented as a spring, he called C;

The height of one story of the building, which he called h [this was an error, as this entity does not enter into the elastic analysis, as explained below];

The mass of the upper part of the building, which he called m;

The acceleration at which bodies fall due to gravity, which he called g;

The force with which the upper part of the building hit the lower part of the building he called Pd;

The force that the lower part of the building could sustain before collapsing he called Po, and claimed it was equal to mg [this is incorrect, as explained below].

Using these entities, he produced Equation (1):

Pd/Po = 1 + The Square Root of the quantity [1 + (2Ch/mg)] ≈ 31

However, Bažant did not explain the process by which he derived this equation, which is an inexplicable omission in a matter of this importance.

Furthermore, there are problems with this equation, which are noted below:

The equation guarantees that Pd was at least twice Po, no matter what the values of the stiffness, mass of the upper part of the building, and height of one story were. This is counterintuitive. How can his equation guarantee this minimum ratio, no matter what the dimensions and properties of the building itself were?

While Bažant’s analysis requires that the upper part of the building fell through one collapsed story prior to the elastic phase of the impact, he uses the fall through this full story height (h) as the elastic deformation. The correct distance for the elastic deformation is only a small fraction of the height of one story.

The factor of “2” was apparently inserted under the radical to represent the two separate springs of the upper and lower parts of the building acting together when the upper part hit the lower part, which would be incorrect, since springs acting in series produce an equivalent stiffness, where 1/Ceq = 1/Cu + 1/CL, [not Cu + CL]. The insertion of the factor “2” in the equation is incorrect.

Bažant also underestimated the design load capacity of the lower part of the building, Po, as mg. However, mg is only the static weight of the previously supported structure above the impact. The columns in the building had safety factors included in their design load capacities: for the perimeter columns it was 5 to 1 and for the core columns it was 3 to 1. Therefore, since the perimeter and core columns essentially shared the static load, Bažant should have used the average of these safety factors, (5 + 3)/2 = 4 for the design load capacity Po = 4mg.

There is no basis for the inclusion of both factors “1” inside and outside the radical, nor is there a basis for taking the square root of a portion of the quantity, as the ratio is simply the elastically generated force (C times the elastic deformation) divided by the design load capacity, (Po = 4mg).

Therefore, the correct form of Equation (1) is:

Pd/Po = (Ceq) X (elastic deformation)/4mg

Using his version of Equation (1), Bažant claimed that the ratio of the force applied by the upper part of the building to the ability of the lower part of the building to sustain that force was approximately 31. This result forms the essential basis for Bažant’s theory, since, according to him, the elastic force that the lower part of the building sustained from the upper part was theoretically enormously greater than its ability to withstand it, which meant that the columns in the lower part of the building must have then gone into inelastic deformation and buckled under the applied load.

He then went on to analyze the inelastic energy dissipation of the collapse mechanism.

But first, his elastic analysis must be corrected. The corrected Equation (1) must be used, and the correct values of the variables must be inserted into it. If the result doesn’t provide a ratio of Pd to Po greater than one, his later inelastic analyses and defenses of his theory are moot, because his theory has failed to prove that an inelastic event took place.

The correction of Bažant’s concept and the errors in equation (1)

As enumerated above, there are unanswered questions regarding Bažant’s Equation (1) to represent the elastic interaction between the upper part of the building and the lower part during his depiction of what caused the buildings to be destroyed.

Bažant’s first error was his conceptualization of the process of destruction. He posited that the upper part of the building acted as a solid body impacting the lower part of the building, with the lower part of the building acting as a spring during the initial elastic impact. He illustrated this concept in Figure 2(a) of his paper [reproduced below], in which the upper part of the building with mass m falls through a distance of one story, h, and impacts the lower part of the building acting as a spring with stiffness C. There are two problems with this concept.

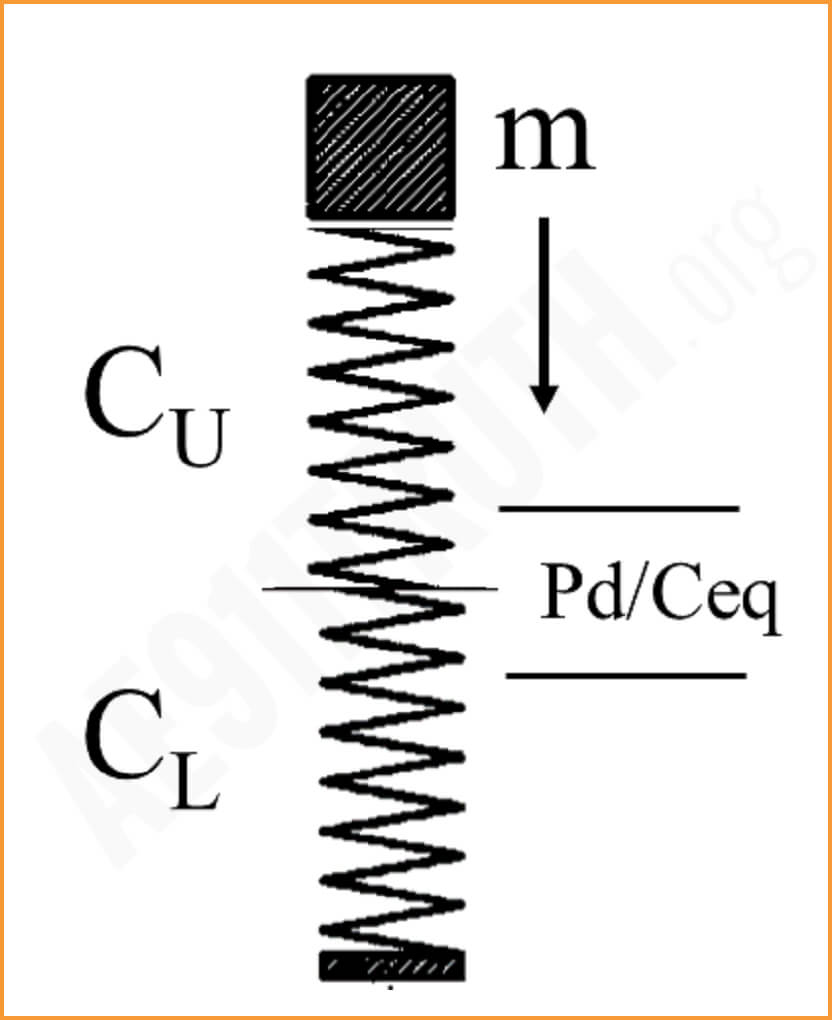
In reality, since for every action there is an equal and opposite reaction, in an elastic reaction the upper part of the building is also acting as a spring under the force of the collision between the two bodies. Therefore, the correct concept of the interaction must include two springs acting in series, each with their own stiffness, whereas Bažant only theorizes one spring – that of the lower part of the building. Correction of his error can be done by calculating the equivalent stiffness of the two springs acting in series, and this concept is also compared to Bažant’s conceptualization below. Bažant’s error affects his mathematical model of the event.

BAŽANT’S FIGURE 2(a)

WHAT BAŽANT’S FIGURE 2(a) SHOULD HAVE BEEN

As noted above, the elastic interaction of the two parts of the building could not involve the descent of the upper portion for a full story, h, of the building. The actual distance could only be the distance due to the compression of the two parts of the building, Pd/Ceq, calculated below, which only amounts to a small fraction of the distance of a full story that Bažant used.

Bažant’s second error was his estimation of the stiffness, C, of the lower part of the building (which is re-labeled CL in the calculations below to correct his equation). Without giving us the details of his calculation for the stiffness of the lower part of the building, he asserted it has an estimated value of 71 GN/m (Giga Newtons per meter). Upon checking this calculation, which Szamboti and MacQueen performed in their paper THE MISSING JOLT³, the actual estimated value of CL was found to be 7.1 GN/m. Thus, Bažant overestimated the stiffness of the lower part of the building by 10X.

The third error was his claim that the downward elastic displacement from the initial equilibrium position to the point of maximum deflection of the lower part of the building was (h + Pd/C). According to Bažant, this would have been a distance of (3.7m + Pd/C). In actuality, in an elastic collision, the deflection would only be Pd/Ceq, and Ceq must be calculated as the equivalent stiffness of the upper and lower springs acting in series, as explained above. Using Szamboti and MacQueen’s method, Pd/Ceq = 7.21 in. = 0.183m.⁴ According to Bažant, the elastic deflection would have been a distance of (3.7m + 0.183m) = 3.883m, but this is incorrect. The height of one story of the building should not have been added to the elastic deformation, Pd/Ceq, because any potential overload causing the complete failure of the columns would only be due to the elastic interaction. Thus, Bažant has overestimated the elastic deformation of the lower part of the building by a factor of 3.883/0.183 = 21.2X.

His fourth error was his estimation of the mass of the upper part of the North Tower as 58 X 10⁶ kg. However, the actual in-service load of the upper part of the building (per NIST it was 12 stories in WTC 1) was 33 X 10⁶ kg.⁵

His fifth error was representing the value of Po = mg as the design load capacity of the lower part of the building. As explained above, mg, the static load, should be increased by the average factor of safety, 4, in order to represent the true design load capacity.

Correcting these errors in Equation (1),

First, finding the equivalent stiffness, Ceq, for the two springs acting in series:

1/Ceq = 1/CL + 1/Cu where CL = stiffness of lower part of the building and Cu = stiffness of upper part of the building

Cu = AE/L where A = approximate cross-section area of columns of upper section (take 97^th floor)

= Core A + Perimeter A = 2,622 in² + 3,726 in² = 6,348 in²

E = 30 X 10⁶ psi and L = height of 12 stories above 97^th floor = 149.24 in X 12 stories = 1,791 in.

Therefore, Cu = 6,348 in² X 30 X 10⁶ psi/1,791 in. = 106.3 X10⁶ lb/in

Converting lb/in to GN/m: 106.3 X 10⁶ lb/in X 4.44 N/lb X 39.37 in/m

Cu = 18.6 GN/m

CL = 7.1 GN/m

1/Ceq = 1/7.1 GN/m + 1/18.6 GN/m and Ceq = 5.14 GN/m

Second, correcting the distance of the elastic deformation by replacing h with the elastic deformation:

Pd/Ceq = 7.21 in

Converting 7.21 inches into meters: 7.21 in X 1 m/39.37 in = 0.183 m

Third, correcting the actual working load of the upper part of WTC 1: m = 33 X 10⁶ kg

And fourth, correcting the capacity of the lower part of the building to withstand the actual design load capacity with factors of safety incorporated,

Po = 4mg (approximately, for perimeter and core columns combined)

Putting these corrected values into Bažant’s Corrected Equation (1) [correcting C by replacing it with Ceq, dropping the 2 under the radical, replacing h with Pd/Ceq and dropping both 1’s and the square root radical]:

Pd/Po = Ceq times the elastic deformation divided by 4mg

Pd/Po = (5.14 GN/m)(0.183 m)/(4)(33 X 10⁶ kg)(9.81 m/sec²)

= 0.73

This is significantly below 1.

Therefore, using Bažant’s corrected Equation (1):

The CDCU theory does not provide a load amplification factor of 31. It actually doesn’t even provide an overload, as the ratio is less than one, and is not large enough to overcome the design load capacity of the lower part of the building to resist collapse.

Collapse would not be initiated and could not occur.

Bažant’s theoretical proof that the elastic response of the lower part of the building cannot withstand the impact of the upper portion of the building is not valid.

Bažant’s theory, when corrected, does not explain the destruction of the Twin Towers.

The remainder of Bažant’s first paper is an analysis of the inelastic energy dissipation caused by the collapse, which is now irrelevant, since the design load capacity of the lower part of the building could not have been overcome by the impact.

The subsequent four papers by Bažant are in defense of his first paper, which has been shown to be incorrect. There is no need to review his subsequent defenses of his theory, as they failed to address his fundamental misconception of the process and the errors noted in his initial analysis. In fact, those efforts specifically reinforced the analysis put forward in the first paper.

For example, in the second paper (JEM March 2007), the following statement is made: “Up to the moment of collapse trigger, the foregoing scenario (impact, removal of fireproofing, heating of members, collapse of floor trusses) was identified by meticulous, exhaustive, and very realistic computer simulations of unprecedented detail, conducted by S. Shyam Sunder’s team at NIST. The subsequent progressive collapse was not simulated at NIST because its inevitability, once triggered by impact after column buckling, had already been proven by Bažant and Zhou’s (2002A) comparison of kinetic energy to energy absorption capability. The elastically calculated stresses caused by impact of the upper part of the tower onto the lower part were found to be 31 times greater than the design stresses…. (…. Eq. 1, rather than 2, is decisive).” (Emphasis added)

In conclusion, the NIST Report purporting to explain the complete collapse of the Twin Towers on 9/11 fails, since it relies on Bažant’s CDCU theory to accurately portray the event, and that theory has been shown to be invalid.

Authors Note: The above appears to be the first time Bažant’s force overload equation has been scientifically challenged publicly and shown to be grossly inaccurate – if the correct equation and input values were used it would not predict a collapse propagation.

However, Bažant’s claims and calculations have previously been shown to be in error from a different perspective. A good example is contained in a technical paper on the subject called “Some Misunderstandings Related to WTC Collapse Analysis”⁶which was published by The International Journal of Protective Structures in June 2013. There the authors showed that if the correct values were used for available impact energy and energy absorption capacity that a collapse would not have propagated and that Bažant’s ratio of these two values was wildly inaccurate.

Both here and in the above-mentioned paper it has been found that Bažant grossly overestimated input values that would be destructive and grossly underestimated input values that would be resistive.

NOTES:

1.Mechanics of Progressive Collapse: Learning from World Trade Center and Building Demolitions, Zdeněk P. Bažant and Mathieu Verdure, Journal of Engineering Mechanics, March 2007; What Did and Did Not Cause Collapse of World Trade Center Twin Towers in New York?, Zdeněk P. Bažant, Jia-Liang Le, Frank R. Greening, and David B. Jenson, Journal of Engineering Mechanics, October 2008; Why the Observed Motion History of World Trade Center Towers is Smooth, Zdeněk P. Bažant and Jia-Liang Le, Journal of Engineering Mechanics, January 2011; Spontaneous Collapse Mechanism of World Trade Center Twin Towers and Progressive Collapse in General, Zdeněk P. Bažant and Jia-Liang Le, Journal of Structural Engineering, April 8, 2022.

2. NIST (National Institute of Standards and Technology). 2005. Federal Building and Fire Safety Investigation of the World Trade Center Disaster: Final Report on the Collapse of the World Trade Center Towers. NIST NCSTAR 1-6 Structural Fire Response and Probable Collapse Sequence of the World Trade Center Towers (authored by John L. Gross and Therese P. McAllister), paragraph 9.4.4, p. 323, wherein they explicitly state (referring to Bažant’s theory), “NIST agrees with the assessment of the tower’s required structural capacity to absorb the released energy of the upper building section as it began to fall as an approximate lower bound.”

NIST also references other studies: Weidlinger Associates, Inc. with Hughes Associates and ArupFire (2002 & 2003); University of Maryland and Israel Institute of Technology (2002); University of Edinburgh (2003 & 2005); and ARUP (2005). However, none of these other reports posited the collapse mechanism of the lower part of the buildings – only Bažant’s paper put forward a theory purporting to explain why the lower part of the buildings failed. Furthermore, in other parts of the NIST Report, references are made to the failure of the lower part of the building for the reasons given in the Bažant theory, e.g., NIST NCSTAR 1, Abstract, p. iii, “Global collapse occurred as potential energy of the falling upper structure exceeded the strain energy capacity of the deforming structural members.”

3. The Missing Jolt, Szamboti & MacQueen, Journal of 9/11 Studies, January 2009, Appendix C.

4. The Missing Jolt, Szamboti & MacQueen, Journal of 9/11 Studies, January 2009, Appendix D.

5. Analysis of the Mass and Potential Energy of World Trade Center Tower 1, Gregory Urich, Journal of 9/11 Studies, December 2007.

6. Some Misunderstandings Related to WTC Collapse Analysis, Gregory Szuladzinski, Anthony Szamboti, Richard Johns, Journal of Protective Structures, June 2013.